확률과 확률분포 (Probability & Distribution)
04 Apr 2020 | Machine-Learning
본 포스트는 문일철 교수님의 인공지능 및 기계학습 개론 I 강의를 바탕으로 작성하였습니다.
Probability & Distribution
Probability (확률)
이번 게시물에서는 확률에 대해서 알아봅시다. 확률(Probability) 이란 무엇일까요? 넓은 의미에서 이 질문에 답을 한다는 것은 쉬운일이 아닙니다. 하지만 ‘수학적’ 확률로 범위를 축소한다면 그리 어려운 문제는 아닙니다. 수학에서의 확률은 아래의 특징을 가지는 함수로 정의할 수 있습니다. 발생 가능한 모든 사건을 나타내는 $\Omega$ 에 대하여 특정 사건 $E$ 의 확률 $P(E)$ 는 아래와 같이 수식으로 나타낼 수 있습니다.
\[P(E) \in R, \quad P(E) \geq 0, \quad P(\Omega) = 1 \\
P(E_1 \cup E_2 \cup ...) = \sum^{\infty}_{i=1} P(E_i) \\
\text{단, } E_i \text{ 가 서로 상호 배타적(Mutually Exclusive)일 경우}\]
확률은 특별한 조건을 가지고 있기 때문에 그로부터 발생하는 몇 가지 특성을 가지고 있습니다.
\[\begin{aligned}
& 1.\quad \text{만약 } A \subset B \text{ 이면 } P(A) \leq P(B) \\
& 2. \quad P(\phi) = 0 \\
& 3. \quad 0 \leq P(A) \leq 1 \\
& 4. \quad P(X \cup Y) = P(X) + P(Y) - P(X \cap Y) \\
& 5. \quad P(E^c) = 1 - P(E)
\end{aligned}\]
첫 번째 특성은 한 사건이 다른 사건의 부분집합일 경우 성립하는 특성입니다. 예를 들면, 주사위를 던져 3이 나오는 사건은 홀수가 나오는 사건의 부분집합입니다. 그렇기 때문에 3이 나올 확률은 홀수가 나올 확률보다 작거나 같습니다. 두 번째 특성은 사건이 공집합일 경우에 대한 특성입니다. 주사위를 던져 7 이상의 눈이 나올 확률이 이에 속합니다. 당연히 0이 되겠습니다. 세 번째 특성은 임의의 사건이 일어날 확률이 $[0,1]$ 사이에 있음을 나타내는 일반적인 성질입니다. 따로 예시는 들지 않도록 하겠습니다.
네 번째는 합집합에 대한 확률입니다. 이번에도 주사위를 던지는 예를 들어봅시다. $X$ 를 소수인 눈이 나오는 사건이라 하고, $Y$ 를 홀수인 눈이 나오는 사건이라고 합시다. 1부터 6까지의 눈 중에서 소수인 눈은 2, 3 으로 2개 이므로 $P(X) = 2/6 =1/3$ 입니다. 또 홀수인 눈은 1, 3, 5 로 3개 이므로 $P(Y) = 3/6 = 1/2$ 입니다. 이제 두 사건의 합사건 $X \cup Y$ 과 곱사건 $X \cap Y$ 을 알아봅시다. 두 사건의 합사건은 1, 2, 3, 5 로 4개 이므로 $P(X \cup Y) = 4/6 = 2/3$ 이고, 곱사건은 두 사건에 동일하게 등장하는 3 하나뿐이므로 $P(X \cap Y) = 1/6$ 입니다. 이를 4번에 나와있는 공식에 대입하면 $2/3 = 1/3 + 1/2 - 1/6$ 으로 공식이 성립한다는 것을 볼 수 있습니다.
마지막은 여집합에 대한 확률입니다. 특정 사건의 확률이 $P(E)$ 일 때, 그 사건이 일어나지 않을 확률 $P(E^c)$ 은 $1 - P(E)$ 임을 특별한 예시 없이도 알 수 있습니다.
Conditional Probability (조건부 확률)
우리가 경험하는 대부분의 사건은 특정 조건하에서 일어납니다. 예를 들면, 오늘 비가 왔을 때 내일 비가 또 올 확률을 구하는 경우가 대표적입니다. 이런 조건(Condition) 은 우리가 특정 확률을 예측하는 데에 필수적인 요건이 됩니다. 1부터 45까지 45개의 번호 중 6개의 번호를 맞추는 로또 번호를 예측하는 경우에도 마찬가지입니다. A라는 사람은 평소에 20번대가 많이 나온다고 생각해서 20번대에 3개의 숫자를 찍을 수도 있습니다. B라는 사람은 지난 주에 나온 숫자가 다시 나올 확률은 적으니 그 숫자를 피할 수도 있고요. 이렇게 우리는 항상 어떤 예측을 할 때, 이전에 어땠는지에 대한 조건을 따져보며 확률을 예측하게 됩니다. 이렇게 조건이 있을 떄의 확률을 조건부 확률(Conditional Probability) 이라고 합니다. 조건부 확률을 구하는 수식은 아래와 같습니다.
\[P(X \vert Y) = \frac{P(X \cap Y)}{P(Y)}\]
위 식에서 $\vert$ 를 기준으로 뒤에 있는 것이 조건입니다. 위에서 나온 주사위의 예를 통해 조건부 확률도 계산해봅시다. 위 4번 공식에서 사용했던 예시를 그대로 사용합니다. 이 예시에서 $P(X \vert Y)$ 를 어떻게 설명할 수 있을까요? $\vert$ 를 기준으로 뒤에 위치한 것이 조건이므로, $P(X \vert Y)$ 는 “주사위를 던져 홀수인 눈이 나왔을 때 그 눈이 소수일 확률” 이 됩니다. 공식을 통해 $P(X \vert Y)$ 의 값을 구하면 $P(X \cap Y) = 1/6, P(Y) = 1/2$ 이므로 $1/3$ 이 됩니다. 실제로도 홀수인 눈이 나오는 경우는 1, 3, 5 이고 그 중 소수인 것은 3이므로 $P(X \vert Y) = 1/3$ 이 맞다는 것을 알 수 있습니다.
해당 공식을 사용하면 아래의 식을 유도할 수 있습니다. 참고로 아래의 식은 베이즈 법칙(Bayes’ Rule) 공식으로 최대 사후 확률 측정(Maximum A Posterior estimation, MAP)을 통해 사건의 확률을 추정하는 데에도 사용됩니다.
\[P(Y \vert X) = \frac{P(X \vert Y)P(Y)}{P(X)}\]
아래의 식도 조건부 확률의 중요한 특성 중 하나입니다. 아래 식에서 $Y_n$ 각각은 각 조건을 나타내며 겹치지 않는 배반사건입니다. 또한 조건 $Y_n$ 을 모두 고려한 경우 전체가 되어야 합니다.
\(P(X) = \sum^n P(X \vert Y_n)P(Y_n) \qquad \text{if} \quad P(Y_i \cap Y_j) = 0 \text{ and } \sum^n Y_i = 1\)
해당 공식의 예시를 들기 위해 다시 이전에 사용했던 예시를 가져와 봅시다. 이번에는 $P(Y_1)$ 을 홀수인 면이 나올 조건, $P(Y_2)$ 를 짝수인 면이 나올 조건이라고 합시다. 이 두 사건은 교집합이 없는 배반 사건이며, 두 사건 이외의 어느 사건도 등장할 수 없습니다. 각 조건에 따르는 조건부 확률 P(X \vert Y_n) 을 구해봅시다. 먼저 $P(X \vert Y_1), P(Y_1)$ 은 이전에 구했던 것과 같이 $1/3, 1/2$ 이므로 $P(X \vert Y_1)P(Y_1) = 1/6$ 입니다. 짝수인 조건 $Y_2$ 에 대해서도 동일한 과정을 수행해봅시다. 짝수의 눈이 나오는 경우의 수는 2, 4, 6으로 3이고 그 중 소수는 2입니다. 이로부터 $P(X \vert Y_2), P(Y_2)$ 는 각각 $1/3, 1/2$ 임을 알 수 있습니다. 그리고 둘의 곱하여 $P(X \vert Y_2)P(Y_2) = 1/6$ 도 구할 수 있습니다. 이제 최종적인 $P(X) = 1/3$ 가 제대로 구해지는지 아래 수식을 따라가며 알아봅시다.
\[P(X) = P(X|Y_1)P(Y_1) + P(X|Y_2)P(Y_2) = 1/6 + 1/6 = 1/3\]
이전의 예시에서 제대로 구해지는 것을 볼 수 있습니다. 다음으로 확률 분포에 대해 알아봅시다.
Probability Distribution (확률 분포)
확률 분포(Probability distribution) 란 확률 변수가 특정한 값을 가질 확률을 나타내는 함수입니다. 이 특정한 값은 연속적(Continuous)일 수도 있고 이산적(Discrete)일 수도 있습니다. 예를 들어, 주사위를 던지는 행위는 확률 변수가 1, 2, 3, 4, 5, 6의 값을 나타내므로 이산 확률 분포(Discrete probability distribution)에 속합니다. 반대로 OO고등학교 학생들의 몸무게를 확률 분포로 나타낸다면 이 값은 연속적인 값을 나타내므로 연속 확률 분포(Continuous probability distribution)를 나타내게 됩니다.
첫 번째로 알아볼 확률 분포는 이항 분포(Binomial distribution) 입니다. 베르누이 시행에 대하여 사건이 나타내는 값이 이산적(Discrete)인 경우를 표현하는 확률분포입니다. 기호로는 $B(n,p)$ 와 같이 나타냅니다. 아래는 이항 분포의 수식 및 확률 질량 함수 그래프를 나타낸 것입니다. 연속적이지 않으므로 점으로 나타나는 것이 특징입니다.
\[f(x;n, p) = \left(\begin{array}{c}n \\k \end{array}\right)p^k (1-p)^{n-k}, \qquad \left(\begin{array}{c}n \\k \end{array}\right) = \frac{n!}{k!(n-k)!} \\
np : \text{mean} \qquad np(1-p) : \text{variance}\]
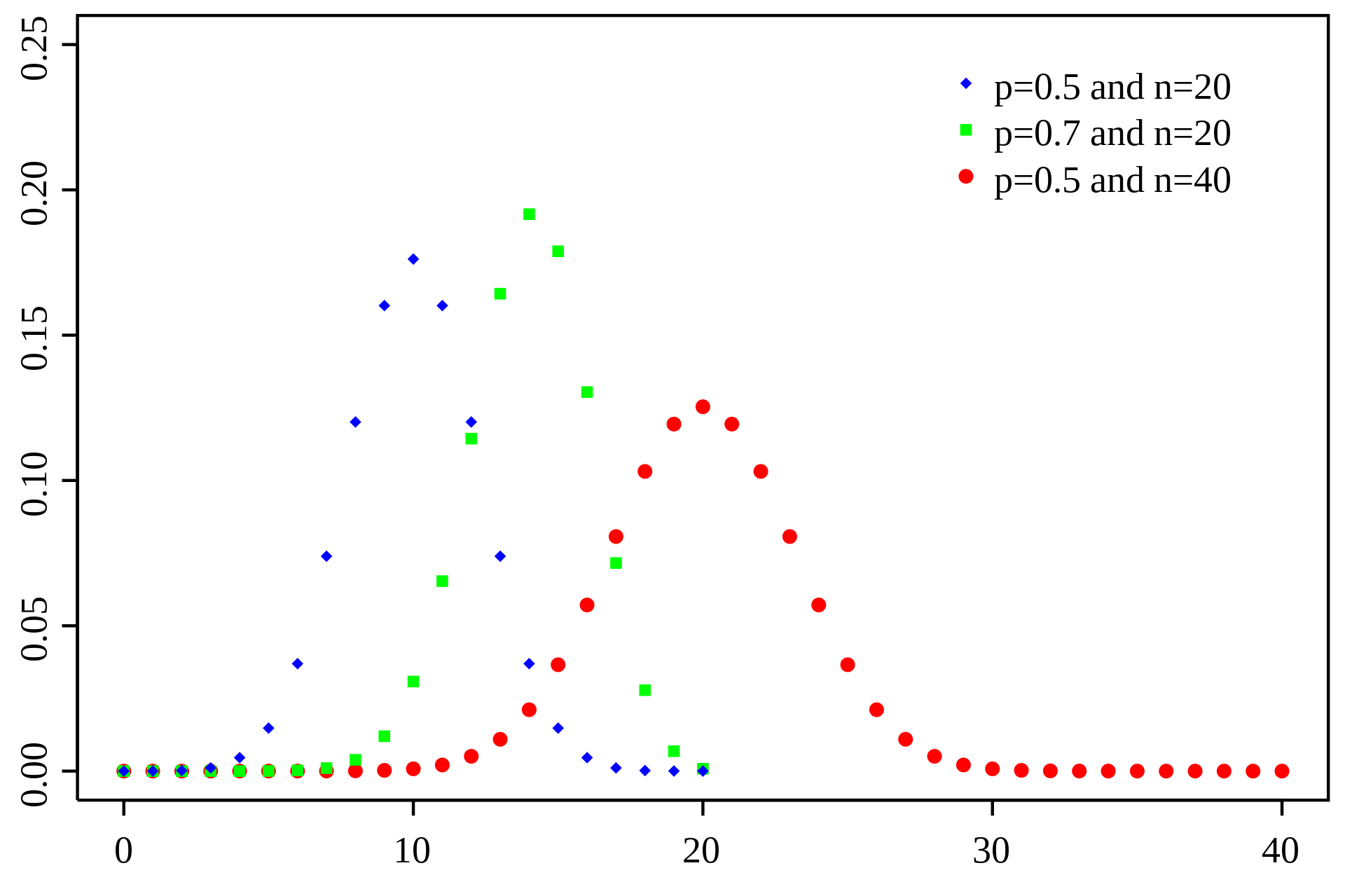
이미지 출처 : 위키피디아 - 이항분포
이항 분포에서 항의 개수를 일반화 하면 다항 분포(Multinomial distribution) 가 됩니다. 다항 분포의 확률 질량 함수 수식은 아래와 같습니다. 주사위를 던지는 경우가 다항 분포를 띠는 대표적인 경우에 속합니다. 실제 Task에서는 언어 생성(Text generation) 모델에서 특정 단어(토큰) 다음에 올 단어를 매 단어마다 예측하게 됩니다. 이것도 여러 이산적인 사건값 중에서 하나를 선택하는 경우이기 때문에 다항 분포에 속한다고 볼 수 있습니다. 기호로는 $\text{Mult}(P), P=<p_1, … , p_k>$ 로 나타냅니다.
\[f(x_1,x_2 ..., x_k; n,p_1,p_2 ..., p_k) = \frac{n!}{x_1!x_2! ... x_k!}p_1^{x_1}p_2^{x_2}...p_k^{x_k} \\
E(x_i) = np_i : \text{mean} \qquad \text{Var}(x_i) = np_i(1-p_i) : \text{variance}\]
다음으로 알아볼 확률 분포는 정규분포(Normal distribution) 입니다. 정규 분포는 가우스 분포(Gaussian distribution) 라는 이름으로도 불립니다. 사건이 연속적인 값을 나타낼 때 쓰이는 연속 확률 분포의 모형 중 하나입니다. 기호로는 $N(\mu, \sigma^2)$ 와 같이 나타냅니다. 위에서 나타난 이산 확률 변수도 부분적으로는 정규분포의 형태를 띠고 있으며 수행 횟수를 더욱 늘린다면 점이 더욱 빽빽하게 찍혀 하나의 선과 비슷하게 나타날 것입니다. 이와 같이 중심극한정리[^1] 에 따라서 독립적인 확률변수의 평균이 정규분포에 가까워지기 때문에 수집된 자료의 분포를 근사하는 데에 정규분포가 자주 사용됩니다.
\[f(x;\mu, \sigma) = \frac{1}{\sigma \sqrt{2 \pi}} \exp \bigg\{-\frac{(x - \mu)^2}{2 \sigma^2}\bigg\} \\
\mu : \text{mean} \qquad \sigma^2 : \text{variance}\]

이미지 출처 : 위키피디아 - 정규분포
세 번째로 알아볼 것은 베타 분포(Beta distribution) 입니다. 베타 분포는 정규 분포와 비슷하게 생겼지만 사건값의 범위가 정해져 있다는 차이가 있습니다. 정규 분포에서 사건값의 범위는 $[-\infty, \infty]$ 입니다. 하지만 베타 분포의 사건값은 $[0,1]$ 범위를 갖습니다. 기호로는 $\text{Beta} (\alpha, \beta)$ 로 나타냅니다. 베타 분포는 특정한 모양을 가지고 있지 않으며 두 매개변수 $\alpha, \beta$ 의 값에 따라서 다양한 모양을 갖습니다. 수식으로는 아래와 같이 나타낼 수 있으며 각 $\alpha, \beta$ 에 따른 그래프는 아래와 같이 생겼습니다.
\[f(\theta; \alpha, \beta) = \frac{\theta^{\alpha-1}(1-\theta)^{\beta-1}}{B(\alpha, \beta)} \\
B(\alpha, \beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}, \quad \Gamma(\alpha) = (\alpha -1)!, \quad \alpha \in N^+ \\
\frac{\alpha}{\alpha + \beta} : \text{mean} \qquad \frac{\alpha\beta}{(\alpha + \beta)^2(\alpha + \beta+1)} : \text{variance}\]
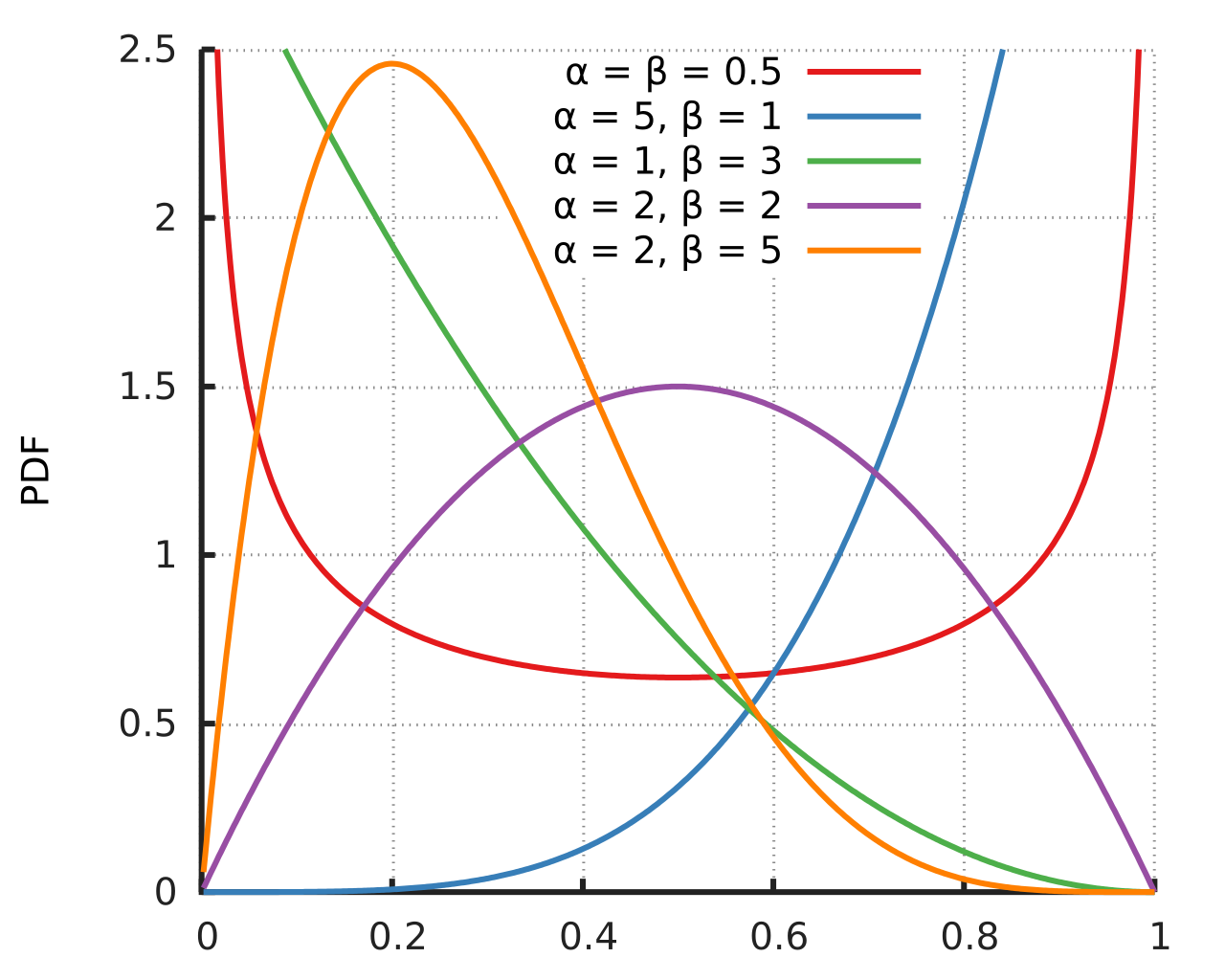
이미지 출처 : 위키피디아 - 베타분포
위에서 알아본 4가지 확률 분포(이항, 다항, 정규, 베타) 외에도 디리클레 분포, 푸아송 분포 등 수많은 확률 분포가 있습니다. 하지만 이번 게시물에서는 이정도만 알아보고 마치는 것으로 하겠습니다.
본 포스트는 문일철 교수님의 인공지능 및 기계학습 개론 I 강의를 바탕으로 작성하였습니다.
Probability & Distribution
Probability (확률)
이번 게시물에서는 확률에 대해서 알아봅시다. 확률(Probability) 이란 무엇일까요? 넓은 의미에서 이 질문에 답을 한다는 것은 쉬운일이 아닙니다. 하지만 ‘수학적’ 확률로 범위를 축소한다면 그리 어려운 문제는 아닙니다. 수학에서의 확률은 아래의 특징을 가지는 함수로 정의할 수 있습니다. 발생 가능한 모든 사건을 나타내는 $\Omega$ 에 대하여 특정 사건 $E$ 의 확률 $P(E)$ 는 아래와 같이 수식으로 나타낼 수 있습니다.
\[P(E) \in R, \quad P(E) \geq 0, \quad P(\Omega) = 1 \\ P(E_1 \cup E_2 \cup ...) = \sum^{\infty}_{i=1} P(E_i) \\ \text{단, } E_i \text{ 가 서로 상호 배타적(Mutually Exclusive)일 경우}\]확률은 특별한 조건을 가지고 있기 때문에 그로부터 발생하는 몇 가지 특성을 가지고 있습니다.
\[\begin{aligned} & 1.\quad \text{만약 } A \subset B \text{ 이면 } P(A) \leq P(B) \\ & 2. \quad P(\phi) = 0 \\ & 3. \quad 0 \leq P(A) \leq 1 \\ & 4. \quad P(X \cup Y) = P(X) + P(Y) - P(X \cap Y) \\ & 5. \quad P(E^c) = 1 - P(E) \end{aligned}\]첫 번째 특성은 한 사건이 다른 사건의 부분집합일 경우 성립하는 특성입니다. 예를 들면, 주사위를 던져 3이 나오는 사건은 홀수가 나오는 사건의 부분집합입니다. 그렇기 때문에 3이 나올 확률은 홀수가 나올 확률보다 작거나 같습니다. 두 번째 특성은 사건이 공집합일 경우에 대한 특성입니다. 주사위를 던져 7 이상의 눈이 나올 확률이 이에 속합니다. 당연히 0이 되겠습니다. 세 번째 특성은 임의의 사건이 일어날 확률이 $[0,1]$ 사이에 있음을 나타내는 일반적인 성질입니다. 따로 예시는 들지 않도록 하겠습니다.
네 번째는 합집합에 대한 확률입니다. 이번에도 주사위를 던지는 예를 들어봅시다. $X$ 를 소수인 눈이 나오는 사건이라 하고, $Y$ 를 홀수인 눈이 나오는 사건이라고 합시다. 1부터 6까지의 눈 중에서 소수인 눈은 2, 3 으로 2개 이므로 $P(X) = 2/6 =1/3$ 입니다. 또 홀수인 눈은 1, 3, 5 로 3개 이므로 $P(Y) = 3/6 = 1/2$ 입니다. 이제 두 사건의 합사건 $X \cup Y$ 과 곱사건 $X \cap Y$ 을 알아봅시다. 두 사건의 합사건은 1, 2, 3, 5 로 4개 이므로 $P(X \cup Y) = 4/6 = 2/3$ 이고, 곱사건은 두 사건에 동일하게 등장하는 3 하나뿐이므로 $P(X \cap Y) = 1/6$ 입니다. 이를 4번에 나와있는 공식에 대입하면 $2/3 = 1/3 + 1/2 - 1/6$ 으로 공식이 성립한다는 것을 볼 수 있습니다.
마지막은 여집합에 대한 확률입니다. 특정 사건의 확률이 $P(E)$ 일 때, 그 사건이 일어나지 않을 확률 $P(E^c)$ 은 $1 - P(E)$ 임을 특별한 예시 없이도 알 수 있습니다.
Conditional Probability (조건부 확률)
우리가 경험하는 대부분의 사건은 특정 조건하에서 일어납니다. 예를 들면, 오늘 비가 왔을 때 내일 비가 또 올 확률을 구하는 경우가 대표적입니다. 이런 조건(Condition) 은 우리가 특정 확률을 예측하는 데에 필수적인 요건이 됩니다. 1부터 45까지 45개의 번호 중 6개의 번호를 맞추는 로또 번호를 예측하는 경우에도 마찬가지입니다. A라는 사람은 평소에 20번대가 많이 나온다고 생각해서 20번대에 3개의 숫자를 찍을 수도 있습니다. B라는 사람은 지난 주에 나온 숫자가 다시 나올 확률은 적으니 그 숫자를 피할 수도 있고요. 이렇게 우리는 항상 어떤 예측을 할 때, 이전에 어땠는지에 대한 조건을 따져보며 확률을 예측하게 됩니다. 이렇게 조건이 있을 떄의 확률을 조건부 확률(Conditional Probability) 이라고 합니다. 조건부 확률을 구하는 수식은 아래와 같습니다.
\[P(X \vert Y) = \frac{P(X \cap Y)}{P(Y)}\]위 식에서 $\vert$ 를 기준으로 뒤에 있는 것이 조건입니다. 위에서 나온 주사위의 예를 통해 조건부 확률도 계산해봅시다. 위 4번 공식에서 사용했던 예시를 그대로 사용합니다. 이 예시에서 $P(X \vert Y)$ 를 어떻게 설명할 수 있을까요? $\vert$ 를 기준으로 뒤에 위치한 것이 조건이므로, $P(X \vert Y)$ 는 “주사위를 던져 홀수인 눈이 나왔을 때 그 눈이 소수일 확률” 이 됩니다. 공식을 통해 $P(X \vert Y)$ 의 값을 구하면 $P(X \cap Y) = 1/6, P(Y) = 1/2$ 이므로 $1/3$ 이 됩니다. 실제로도 홀수인 눈이 나오는 경우는 1, 3, 5 이고 그 중 소수인 것은 3이므로 $P(X \vert Y) = 1/3$ 이 맞다는 것을 알 수 있습니다.
해당 공식을 사용하면 아래의 식을 유도할 수 있습니다. 참고로 아래의 식은 베이즈 법칙(Bayes’ Rule) 공식으로 최대 사후 확률 측정(Maximum A Posterior estimation, MAP)을 통해 사건의 확률을 추정하는 데에도 사용됩니다.
\[P(Y \vert X) = \frac{P(X \vert Y)P(Y)}{P(X)}\]아래의 식도 조건부 확률의 중요한 특성 중 하나입니다. 아래 식에서 $Y_n$ 각각은 각 조건을 나타내며 겹치지 않는 배반사건입니다. 또한 조건 $Y_n$ 을 모두 고려한 경우 전체가 되어야 합니다. \(P(X) = \sum^n P(X \vert Y_n)P(Y_n) \qquad \text{if} \quad P(Y_i \cap Y_j) = 0 \text{ and } \sum^n Y_i = 1\)
해당 공식의 예시를 들기 위해 다시 이전에 사용했던 예시를 가져와 봅시다. 이번에는 $P(Y_1)$ 을 홀수인 면이 나올 조건, $P(Y_2)$ 를 짝수인 면이 나올 조건이라고 합시다. 이 두 사건은 교집합이 없는 배반 사건이며, 두 사건 이외의 어느 사건도 등장할 수 없습니다. 각 조건에 따르는 조건부 확률 P(X \vert Y_n) 을 구해봅시다. 먼저 $P(X \vert Y_1), P(Y_1)$ 은 이전에 구했던 것과 같이 $1/3, 1/2$ 이므로 $P(X \vert Y_1)P(Y_1) = 1/6$ 입니다. 짝수인 조건 $Y_2$ 에 대해서도 동일한 과정을 수행해봅시다. 짝수의 눈이 나오는 경우의 수는 2, 4, 6으로 3이고 그 중 소수는 2입니다. 이로부터 $P(X \vert Y_2), P(Y_2)$ 는 각각 $1/3, 1/2$ 임을 알 수 있습니다. 그리고 둘의 곱하여 $P(X \vert Y_2)P(Y_2) = 1/6$ 도 구할 수 있습니다. 이제 최종적인 $P(X) = 1/3$ 가 제대로 구해지는지 아래 수식을 따라가며 알아봅시다.
\[P(X) = P(X|Y_1)P(Y_1) + P(X|Y_2)P(Y_2) = 1/6 + 1/6 = 1/3\]이전의 예시에서 제대로 구해지는 것을 볼 수 있습니다. 다음으로 확률 분포에 대해 알아봅시다.
Probability Distribution (확률 분포)
확률 분포(Probability distribution) 란 확률 변수가 특정한 값을 가질 확률을 나타내는 함수입니다. 이 특정한 값은 연속적(Continuous)일 수도 있고 이산적(Discrete)일 수도 있습니다. 예를 들어, 주사위를 던지는 행위는 확률 변수가 1, 2, 3, 4, 5, 6의 값을 나타내므로 이산 확률 분포(Discrete probability distribution)에 속합니다. 반대로 OO고등학교 학생들의 몸무게를 확률 분포로 나타낸다면 이 값은 연속적인 값을 나타내므로 연속 확률 분포(Continuous probability distribution)를 나타내게 됩니다.
첫 번째로 알아볼 확률 분포는 이항 분포(Binomial distribution) 입니다. 베르누이 시행에 대하여 사건이 나타내는 값이 이산적(Discrete)인 경우를 표현하는 확률분포입니다. 기호로는 $B(n,p)$ 와 같이 나타냅니다. 아래는 이항 분포의 수식 및 확률 질량 함수 그래프를 나타낸 것입니다. 연속적이지 않으므로 점으로 나타나는 것이 특징입니다.
\[f(x;n, p) = \left(\begin{array}{c}n \\k \end{array}\right)p^k (1-p)^{n-k}, \qquad \left(\begin{array}{c}n \\k \end{array}\right) = \frac{n!}{k!(n-k)!} \\ np : \text{mean} \qquad np(1-p) : \text{variance}\]
이미지 출처 : 위키피디아 - 이항분포
이항 분포에서 항의 개수를 일반화 하면 다항 분포(Multinomial distribution) 가 됩니다. 다항 분포의 확률 질량 함수 수식은 아래와 같습니다. 주사위를 던지는 경우가 다항 분포를 띠는 대표적인 경우에 속합니다. 실제 Task에서는 언어 생성(Text generation) 모델에서 특정 단어(토큰) 다음에 올 단어를 매 단어마다 예측하게 됩니다. 이것도 여러 이산적인 사건값 중에서 하나를 선택하는 경우이기 때문에 다항 분포에 속한다고 볼 수 있습니다. 기호로는 $\text{Mult}(P), P=<p_1, … , p_k>$ 로 나타냅니다.
\[f(x_1,x_2 ..., x_k; n,p_1,p_2 ..., p_k) = \frac{n!}{x_1!x_2! ... x_k!}p_1^{x_1}p_2^{x_2}...p_k^{x_k} \\ E(x_i) = np_i : \text{mean} \qquad \text{Var}(x_i) = np_i(1-p_i) : \text{variance}\]다음으로 알아볼 확률 분포는 정규분포(Normal distribution) 입니다. 정규 분포는 가우스 분포(Gaussian distribution) 라는 이름으로도 불립니다. 사건이 연속적인 값을 나타낼 때 쓰이는 연속 확률 분포의 모형 중 하나입니다. 기호로는 $N(\mu, \sigma^2)$ 와 같이 나타냅니다. 위에서 나타난 이산 확률 변수도 부분적으로는 정규분포의 형태를 띠고 있으며 수행 횟수를 더욱 늘린다면 점이 더욱 빽빽하게 찍혀 하나의 선과 비슷하게 나타날 것입니다. 이와 같이 중심극한정리[^1] 에 따라서 독립적인 확률변수의 평균이 정규분포에 가까워지기 때문에 수집된 자료의 분포를 근사하는 데에 정규분포가 자주 사용됩니다.
\[f(x;\mu, \sigma) = \frac{1}{\sigma \sqrt{2 \pi}} \exp \bigg\{-\frac{(x - \mu)^2}{2 \sigma^2}\bigg\} \\ \mu : \text{mean} \qquad \sigma^2 : \text{variance}\]
이미지 출처 : 위키피디아 - 정규분포
세 번째로 알아볼 것은 베타 분포(Beta distribution) 입니다. 베타 분포는 정규 분포와 비슷하게 생겼지만 사건값의 범위가 정해져 있다는 차이가 있습니다. 정규 분포에서 사건값의 범위는 $[-\infty, \infty]$ 입니다. 하지만 베타 분포의 사건값은 $[0,1]$ 범위를 갖습니다. 기호로는 $\text{Beta} (\alpha, \beta)$ 로 나타냅니다. 베타 분포는 특정한 모양을 가지고 있지 않으며 두 매개변수 $\alpha, \beta$ 의 값에 따라서 다양한 모양을 갖습니다. 수식으로는 아래와 같이 나타낼 수 있으며 각 $\alpha, \beta$ 에 따른 그래프는 아래와 같이 생겼습니다.
\[f(\theta; \alpha, \beta) = \frac{\theta^{\alpha-1}(1-\theta)^{\beta-1}}{B(\alpha, \beta)} \\ B(\alpha, \beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}, \quad \Gamma(\alpha) = (\alpha -1)!, \quad \alpha \in N^+ \\ \frac{\alpha}{\alpha + \beta} : \text{mean} \qquad \frac{\alpha\beta}{(\alpha + \beta)^2(\alpha + \beta+1)} : \text{variance}\]
이미지 출처 : 위키피디아 - 베타분포
위에서 알아본 4가지 확률 분포(이항, 다항, 정규, 베타) 외에도 디리클레 분포, 푸아송 분포 등 수많은 확률 분포가 있습니다. 하지만 이번 게시물에서는 이정도만 알아보고 마치는 것으로 하겠습니다.

Comments